Vous êtes en seconde et les fonctions vous semblent être un mystère ? Pas de panique ! Découvrons ensemble ce monde fascinant des fonctions de référence, ces outils mathématiques essentiels pour comprendre et modéliser des situations de la vie courante.
Les fonctions de référence en seconde, comme la fonction affine, la fonction carré et la fonction inverse, sont les pierres angulaires de l'analyse mathématique. Elles servent de base à la compréhension de concepts plus complexes que vous aborderez dans les classes supérieures. Maîtriser ces fonctions vous permettra d'analyser des graphiques, de résoudre des équations et d'interpréter des données.
L'histoire des fonctions remonte à l'Antiquité, avec des traces de leur utilisation chez les Babyloniens et les Égyptiens. Leur formalisation mathématique a évolué au fil des siècles, notamment grâce aux travaux de mathématiciens comme Descartes et Leibniz. L'importance des fonctions de référence réside dans leur capacité à modéliser des phénomènes variés, qu'il s'agisse de la trajectoire d'un projectile, de la croissance d'une population ou de la variation d'une température.
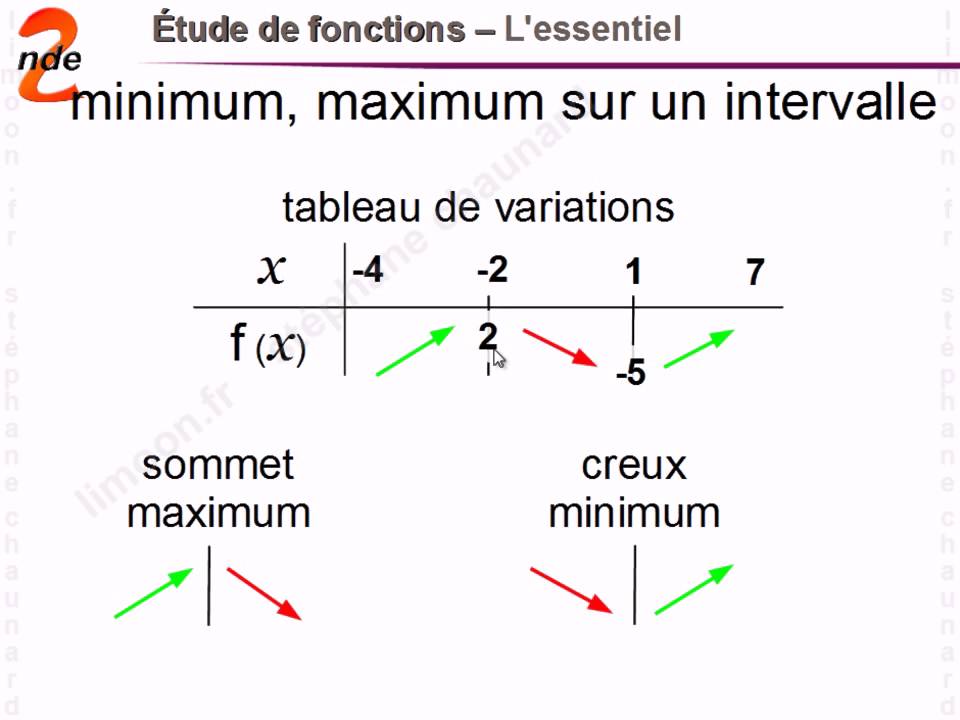
Un des problèmes majeurs rencontrés par les élèves avec les fonctions est la difficulté à visualiser leur comportement graphique. Il est important de comprendre le lien entre l'équation d'une fonction et la forme de sa courbe représentative. Par exemple, la fonction carré, f(x) = x², est représentée par une parabole, tandis que la fonction inverse, f(x) = 1/x, est représentée par une hyperbole.
Prenons la fonction affine, f(x) = ax + b. 'a' représente le coefficient directeur, qui détermine la pente de la droite, et 'b' représente l'ordonnée à l'origine, c'est-à-dire le point où la droite coupe l'axe des ordonnées. Si a > 0, la fonction est croissante, si a < 0, elle est décroissante. Par exemple, f(x) = 2x + 1 est une fonction affine croissante.
Les fonctions de référence offrent de nombreux avantages. Premièrement, elles permettent de modéliser des situations réelles. Deuxièmement, elles facilitent la résolution de problèmes mathématiques complexes. Troisièmement, elles constituent une base solide pour l'apprentissage de concepts mathématiques plus avancés.
Voici quelques questions fréquemment posées sur les fonctions de référence :
1. Qu'est-ce qu'une fonction affine ? Réponse : Une fonction dont la représentation graphique est une droite.
2. Comment déterminer le coefficient directeur d'une fonction affine ? Réponse : En calculant la variation de y divisée par la variation de x.
3. Qu'est-ce que la fonction carré ? Réponse : Une fonction de la forme f(x) = x².
4. Qu'est-ce que la fonction inverse ? Réponse : Une fonction de la forme f(x) = 1/x.
5. Comment représenter graphiquement une fonction ? Réponse : En traçant des points dans un repère cartésien.
6. Comment résoudre une équation avec une fonction ? Réponse : En utilisant des méthodes algébriques ou graphiques.
7. Comment interpréter le graphique d'une fonction ? Réponse: En analysant sa forme, ses variations et ses points clés.
8. Où puis-je trouver des exercices sur les fonctions ? Réponse : Dans votre manuel scolaire, sur des sites web éducatifs ou dans des applications dédiées aux mathématiques.
Un conseil : n'hésitez pas à utiliser des outils de visualisation graphique, comme GeoGebra, pour mieux comprendre le comportement des fonctions.
En conclusion, les fonctions de référence en seconde sont des outils essentiels pour votre parcours mathématique. Elles vous permettent de modéliser, d'analyser et de résoudre des problèmes. Maîtriser ces concepts vous ouvrira les portes vers des domaines plus complexes et passionnants des mathématiques. N'hésitez pas à pratiquer régulièrement et à poser des questions à votre professeur pour solidifier vos connaissances. L'apprentissage des fonctions peut sembler ardu au début, mais avec de la persévérance, vous découvrirez toute leur puissance et leur utilité. Alors, lancez-vous et explorez le monde fascinant des fonctions !
Analyses medicales a frasnes votre guide complet
Voyage toulouse nice en train un guide complet
Le secret des plats principaux saveurs et traditions culinaires